Dr. Irene Pepperberg explores the question, "Can a parrot understand probability?" Drawing on Piagetian cognitive tasks originally designed for children, Dr. Pepperberg and her team tested whether a Grey parrot, Griffin, could grasp the concept of probability. In this blog, we’ll dive into Dr. Pepperberg’s research, where she shares how Griffin’s performance on a probability task reveals intriguing evidence of probabilistic reasoning in parrots. Could parrots really understand concepts like "more likely" and "less likely"? Let’s find out!

Can A Parrot Understand Probability As A Concept?

Here, to solve the question, "Can a parrot understand probability?" Dr. Pepperberg. She starts by saying, "A few months ago, I wrote about Piagetian liquid conservation, noting that, in order to create experiments for our parrots, I often adapt tasks that were initially designed to examine how children develop various cognitive skills.

Sometimes, I'm not the one who does the adaptation. As a final paper in one of my courses, a student presented a draft of how we could examine another Piagetian task, one involving an understanding of probability. The paper was so good that I asked her to join the lab and carry out the experiment. She—and the birds and other students involved—obtained excellent results, and the paper has recently been accepted for publication (Pepperberg et al., 2018). I'll provide a brief summary here."

Dr. Pepperberg goes on to explain that probability is one of the most difficult concepts for humans to understand fully. Children have to be about twelve years old before they succeed in some of Piaget's probability tasks, and even some adults never quite understand probability. (Think about how few people can appropriately solve the "Monty Hall" problem—look it up on the Internet!) They didn't test Griffin on tasks designed for the oldest children but rather used those for the 6-8-year-olds, given that he matched that age group on the previous conservation task.

She says, "The task seems pretty simple: If I put three blue balls and one red one in a bucket, mix them around, grab one in my hand, and, while my hand is still closed, ask you what colour you think I have, you'd probably say "blue". Your reasoning is basically "more is more likely." But until children are over 6 years old, they say things like "Red, because it's my favourite colour," or "OK, you put one red one in and took one out, so it has to be red." Only later do they say things like "Blue, 'cause it's the mostest." 

However, if I repeated the task over and over and over and asked the same question again and again, once in a while, you'd also say "red", figuring the draw can't always be blue. At some level, you'd be correct in that even though there are more blue than red balls, you have no guarantee that blue will be drawn, only that it will be drawn more times than red. But how do you actually decide what to do?"

Well, it depends on the number of trials you are given, how well you understand statistics, and what are your goals. For a very small number of trials, most people stick with the majority … "more" definitely is "more likely." And, if you fully understand statistics and are betting to win over the course of lots of trials, you should again stick with the majority… in 100 trials, for example, if you stick with the majority, you will be correct ~75% of the time, and that's as good as it gets.

If you are a typical adult human, however, you are likely to try probability matching or sampling: you guess blue most of the time but try red about 25% of the time, based on the knowledge that red will come up at that percentage (i.e., has to come up some of the time if the draw is not fixed)—but, because you really can't correctly guess when red actually will come up, you won't do as well as if you stuck with the majority. Still, probability matching is not an awful strategy; it's a lot better than guessing randomly and makes intuitive, if not statistical, sense.

Griffin Put To The Test

The question was, what would Griffin do? Because he could label objects, we gave him essentially the same task as the children, using three of one item and one of another, and asked what the removed, hidden item was likely to be. 

The picture below shows how we performed the task. We used several different sets of objects (e.g., pieces of cork and pieces of wood, pieces of paper and woollen pompons) and randomly switched the sets and what would be the majority and minority items. We put in lots of controls to ensure that we weren't using him and gave him 96 trials (the number needed to balance all the different sets and majority/minority switches).

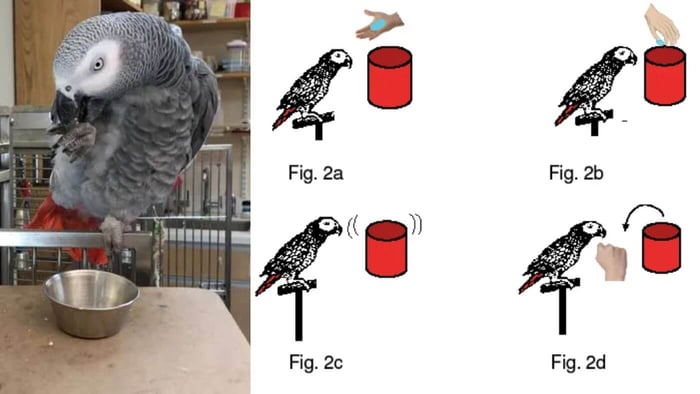
He could have used one of three different strategies: (a) choose at random because he had no idea what was drawn (the least intelligent and simplest strategy); (b) choose the majority item 100% of the time (showing that he understood statistics, but in a sense, a fairly simple strategy in that he would have just stayed with "more" is "more likely"); or (c) try to match the probability, choosing the majority 75% and the minority 25% of the time (not very good statistically, but ecologically sound in that "more" does not guarantee "more likely").

Griffin's Guesses

Interestingly, like most adult humans and children about 8 years old, he used (c). He chose the majority, 76%, and the minority, 24% of the time. He updated answers based on the information he acquired from the previous trials, predicting the identity of a sample drawn from a population of a known composition. 

Such behaviour reflects an intriguing form of probabilistic reasoning: He gave more consideration to the hypothesis that the most prevalent object is the most likely but also some consideration to the least prevalent.

Griffin both estimated the distribution of items in the environment and—critically, with respect to full probabilistic reasoning as described by Piaget and Inhelder (1975)—recognised that even a favourable proportion does not guarantee a particular outcome (demonstrating Piaget and Inhelder's Stage II abilities). Of course, one can argue that (b) is the optimal strategy…but it generally takes a formal course in statistics in order to figure that out!

This aligns with findings from studies on other parrot species, such as the Kaka parrot, which have shown that even older parrots can learn new tricks and adapt to challenges. These insights highlight the advanced problem-solving abilities and cognitive flexibility of parrots, underscoring their remarkable intelligence.

So we ask again, "Can a parrot understand probability?" Interestingly enough, it seems so!

Clements, K., Gray, S.L., Gross, B., & Pepperberg, I.M. (2018). Initial evidence for probabilistic learning by a Grey parrot (Psittacus erithacus). Journal of Comparative Psychology. .doi: 10.1037/com0000106

Piaget, J., & Inhelder, B. (1975). The origin of the idea of chance in children (L. Leake, Trans.). New York, NY: Norton.

This article was originally published by Lafeber.